Original post was published on Veracode blog here

This is the ninth entry in blog series on using Java Cryptography securely. We started off by looking at the basics of Java Cryptography Architecture, assembling one crypto primitive after other in posts on Cryptographically Secure Random Number Generator, symmetric & asymmetric encryption/decryption & hashes. In the meantime, we had to catchup with cryptographic update in latest versions of Java. Having looked at some of the most common symmetric cryptography based applications a.k.a. Message Authentication Codes and Password Storage, let’s take a slight diversion and look at asymmetric cryptography applications starting with Digital Signatures in this post.

Skip to the TL;DR

Overview: What Is a Digital Signature

Digital Signatures are in many ways analogous to physical signatures, providing assurance to the receiver that the received message was created and sent by claimed sender (authentication), binds sender to the data in the received message (non-repudiation) and message was received unaltered (integrity). It doesn’t provide any confidentiality of the messages being exchanged.

Digital Signatures are asymmetric key based operation, in which private key is used to digitally sign a message and corresponding public key is used to verify the signature. Message Authentication Code as well as Digital Signatures both are used for signing messages. MACs are generated and verified by a shared symmetric key, in contrast digital signature is generated by PrivateKey generated by Asymmetric Encryption (public key cryptography) and verified only by the corresponding PublicKey. This private key would be possessed only by the signing authority. Thus, Digital Signatures provide non-repudiation service which MAC can’t.

HowTo: How Does It Work?

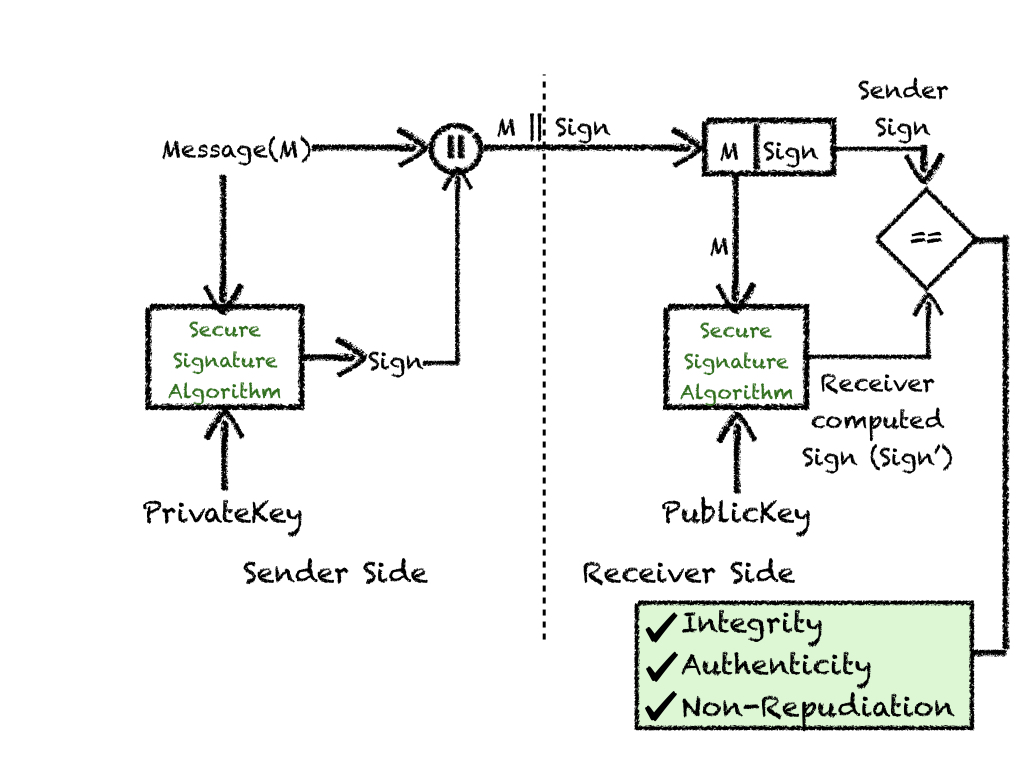
Similar to Message Authentication Codes (MAC), core concept of digital signature revolves around, computing signature on the sender side using PrivateKey applied on hash of the message(M), sending original message and computed signature to receiver. Receiver verifies the signature using PublicKey. If signatures match, non- repudiation, authenticity and integrity of message from intended sender has been verified.

Digital Signature Steps:

Asymmetric Keys; PrivateKey and PublicKey are generated. Sender safely stores PrivateKey, PublicKey is publicly available.
Sender computes Sign of message(M): Sign = SignatureAlgorithm(M, PrivateKey, Hash Algorithm).
M || Sign sent to reciever.
On receiver side, Sign is verified by computing: Sign' = SignatureAlgorithm(M,PublicKey,Hash Algorithm).
If Sign == Sign' , non-repudiation, authenticity and integrity of message from intended sender has been verified.

HowTo: Construction of a Digital Signature

Digital Signatures

HowTo: Design

Before we dive into full-fledged implementation discussions, we need to make a few design decisions:

HowTo: Decide Which Signature Algorithm to Choose?

RSA has been de-facto algorithm being used in Digital Signature. However, over time it has been proved fragile^[9]. DSA is on its path of deprecation^[4] in favor of ECDSA. By steering clear of these two Signature algorithms, we would eliminate more than 50% of Signature algorithms supported by JCA.

As we were discussing in our Java Crypto Catch-up post, later Java versions provide us with very mature Elliptic Curve (ECC) support, we should be embracing those schemes. If you want to learn more about how ECC works and compares against other public key generation mechanisms, I have listed some links in references section below.

Over time there are many curves floating around, not all are good for cryptographic purposes. You should pick between:

Edward Curves: For any new development, I would suggest using Edward Curve based schemes. Both Ed25519 and Ed448 schemes provided by JCA are excellent options. Not yet standardized by government authorities (NIST), but it’s on its way.
NIST Standardized Curves: If at all^[11], you have to abide by government standards, go for ECDSA with an approved curve providing at least 128 bits of security strength. But how to choose a secure curve from 25 options provided through ECGenParameterSpec transparent specification? Below are some of secure parameter spec you should choose^[3][5][8] from:

sect283r1
sect409r1
sect571r1
secp256r1
secp384r1
secp521r1
sect233r1
secp224r1

Note: Prefer using curves where internal domain parameters are randomized (second to last character is ‘r’)^[7].

Summarizing,

Choose Edward Curves as Signature Algorithm. If you have to abide by NIST standards, choose a curve providing at least 128 bits of security strength.

HowTo: Decide Underlying Hashing Algorithm?

Signature schemes underneath typically generate a cryptographic hash of the original message and then apply signing algorithm on this hash. Depending on which type of curve you decide on using:

Edward Curve:

Good news is the hashing algorithm is decided by the scheme^[6] :). You don’t have to do anything extra.

NIST Standardized Curve:

You have to choose an underlying hash providing at least 112 bit of security strength. Below are all safe hashing choices:

SHA224
SHA256
SHA384
SHA512
SHA3-224
SHA3-256
SHA3-384
SHA3-512

Choose SHA2 or SHA3 family of hashing algorithm while working with ECDSA Signature Scheme.

Note: For ECDSA, make sure you pick a scheme that has a hashing algorithm specified. NONEwithECDSA is not a safe option. Also, don’t pick any ambiguous names like simply ECDSA, depending on the provider it might lead to an insecure option, such as SHA1withECDSA.

HowTo: Implement

Bringing all this together, let’s start looking at how to implement the above steps using both Edward Curves and NIST standardized curves:

Step 1: Generating Asymmetric Keys: As we discussed in Encryption/Decryption post, we would need to tap upon KeyPairGenerator class to generate asymmetric keys to be used with your curves. By using ECC based Signatures, you have escaped the complexity of configuring secure parameters such as keysizes and randomness sources, while generating a KeyPair. ECC implementation does that for you.

Edward Curves:

KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("Ed25519"); // Initialize to generate asymmetric keys for use with Edward Curves
KeyPair keyPair = keyPairGenerator.generateKeyPair(); // generate asymmetric keys

NIST Standardized Curves: We need to specify which curve to use thru transparent specification in ECGenParameterSpec class:

KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("EC"); // Initialize to generate asymmetric keys to be used with one of the Elliptic Curve algorithms
ECGenParameterSpec egps = new ECGenParameterSpec("secp384r1"); // using domain parameters specified by safe curve spec of secp384r1
Keypair keyPair = keyPairGenerator.generateKeyPair(); // Generate asymmetric keys.

Congratulations! The hardest part of implementing a digital signature scheme is behind us.

Step 2: Generating Signature on sender side: Signature class provides all what we need. Depending on the curve used, make sure correct algorithm is being configured with Signature class. For e.g.,
- Edward Curves:
```
Signature sign = Signature.getInstance("Ed25519"); // Ed25519 Signature algorithm to be 
```
- NIST Standardized Curves:
```
Signature sign = Signature.getInstance("SHA512withECDSA"); // Signature algorithm is initialized 
```

Once you have asymmetric keys generated and Signature object initialized, it is time to sign the message. This part is the same irrespective of the curve you choose.

sign.initSign(keyPair.getPrivate()); // Initialize Signature object with Private Key 
sign.update(message.getBytes()); // Update the whole message to be signed. If needed do a buffered reading. 
byte[] signArray = signArray = sign.sign(); // Actually sign the message. signArray, holds the actual signature.

Step 3: Signature sent on receiver side: signArray is what holds the actual signature which is appended with the original message and sent on the receiver side.
Step 4 & 5: Verifying Signature on Receiver Side: Signature object is initialized with the same algorithm as used on sender side:

Signature verify = Signature.getInstance(Ed25519 | SHA512withECDSA); // Pick whichever used on sender side

Verification process:

verify.initVerify(keyPair.getPublic());
verify.update(message.getBytes());
boolean isVerified = verify.verify(signArray); // if true, authenticity, integrity and non-repudiation of sender and message verified. This method computes the signature on receiver side as well.

Note: To keep code snippets cleaner, some key, byte array & exception handling details are omitted. Complete working examples can be referred at EdDigitalSignatureAPI.java and ECDigitalSignatureAPI.java for Edward Curves and NIST Standard Curves respectively.

HowTo: Do’s and Don’ts

Do’s:

Embrace Elliptic Curve based Signature Algorithms.
Use Edward Curves Ed25519 or Ed448. If using NIST standardized curves, pick which provides at least 112 bits of security.
Use SHA2 or SHA3 family of underlying hash algorithm.

Don’ts:

Don’t use MD5 or SHA1 as underlying hash algorithm.
Don’t use ambiguous signature algorithm names like ECDSA.

HowTo: Decide Where to Use it (Applications)?

Applications of Digital Signatures ranges from secure communication to code signing to signing blockchain transactions. Digital Signatures are a fundamental building block in any Public Key Infrastructure(PKI)^[10] system. PKI coupled with Certificate Authorities & Digital Certificates makes https, secure emails, certificate-based authentication in your microservice’s service-mesh and many other applications needing authenticity and integrity possible.

Public Key Cryptography is a vast, complicated section of Cryptography. This post hopefully gives you adequate knowledge to get you started using Digital Signature applications. Hang in there for some more Crypto!

You can experiment with generating and verifying signatures by invoking corresponding endpoints from Java Crypto MicroService.

TL;DR

Digital Signatures are cryptographic checksums generated using asymmetric cryptography providing non-repudiation, authenticity and integrity cryptographic services.
Use Elliptic Curve (Edward Curves or a secure NIST standardized curve) based Signature Algorithms, with SHA2 or SHA3 families of underlying hash algorithms.
Applications of Signatures ranges from any secure communication protocols, code signing, cryptocurrencies and Public Key Infrastructure.